Symmetric Kruskal Tensors

>> Tensor Toolbox >> Tensor Types >> Symmetric Kruskal Tensors

A symmetric Kruskal tensor is a decomposition of a tensor into a sum of vector outer products. The symmetric structure means that each term in the summand is the outer product of a single vector with itself 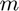$m$ times, where 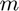$m$ is the number of modes of the decomposed tensor. This contrasts with a generic Kruskal tensor, where each summand is an outer product of m different vectors. More concisely, a symmetric Kruskal tensor decomposition of a tensor 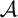$\mathcal{A}$ has the following form:

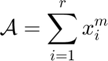
$$\mathcal{A} = \sum_{i=1}^{r} x_{i}^{m}$$

In this notation, a subscript refers to a column index. A superscript refers to the outer product of a single vector with itself 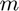$m$ times.

$$x^{m} = \underbrace{x \circ x \circ ... \circ x}_{\mbox{m-times}}.$$

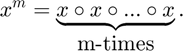
The number of summands in the decomposition, 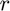$r$, is referred to as the number of components of the symmetric Kruskal tensor.

An alternative, often equivalent expression for a symmetric Kruskal tensor decomposition specifies a real-valued weight for each of the summands in the outer product. The 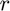$r$-vector formed by these weights is referred to as the weight or lambda vector of the symmetric Kruskal decomposition.

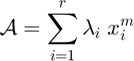
$$\mathcal{A} = \sum_{i=1}^{r} \lambda_{i} \; x_{i}^{m}$$

In certain cases the lambda vector is required in order for a symmetric Kruskal decomposition to exist, e.g. when a symmetric Kruskal tensor has an even number of components and the tensor to be decomposed has a negative element on its main diagonal. In many other cases, the lambda vector is optional and the symmetric Kruskal decomposition can be represented without specifying a lambda vector.

The symktensor class stores symmetric Kruskal tensors, and exploits the extra symmetric structure to perform many calculations more efficiently.

Contents

Declaring a symmetric Kruskal tensor with symktensor

The symktensor format stores the vectors and weights of a symmetric Kruskal tensor decomposition. The vectors in the decomposition are collected as the columns of a matrix X, referred to as the factor matrix. The lambda vector, containing the (often optional) weights is input into the constructor as a column vector. The lambda vector and factor matrix are collectively referred to as the constituent parts in the declaration of a symktensor. For example, consider the decomposition of a tensor 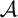$\mathcal{A}$.

$$\mathcal{A} = \sum_{r} \lambda_{r} \; x_{r}^{m}$$

In the example that follows, we form a symmetric Kruskal decomposition by specifying a factor matrix, lambda vector, and the number of modes of the decomposed tensor. We pass all three arguments to the symktensor constructor. This can be stored as a symmetric Kruskal tensor as follows.

n = 4; %The dimension in each mode of the tensor A
m = 3; %The number of modes of A
r = 2; %The rank of the decomposition
X = reshape(1:n*r,n,r); %The columns of this matrix are the vectors in decomposition
L = [1; -1]; %the weights (should be a column vector of length r)
S = symktensor(L, X, m) %Declare a symktensor object

S is a symktensor of order 3 and dimension 4
	S.lambda = [ 1 -1 ]
	S.U = 
		     1     5
		     2     6
		     3     7
		     4     8

A symktensor object can be declared without a weight vector by specifiying the number of modes, the rank, and an additional 'nolambda' option. In this case, the lambda vector is set to a vector of all ones.

S2 = symktensor(X, m, r, true)

S2 is a symktensor of order 3 and dimension 4
	S2.lambda = [ 1  1 ]
	S2.U = 
		     1     5
		     2     6
		     3     7
		     4     8

A random symktensor object can be declared by passing the constructor two arguments: the rank of the decomposition and a tensor or symtensor (for size). The lambda vector is taken to be all ones, and the factor matrix has elements drawn uniformly from (0,1).

T1 = tensor(n*ones(1,m)); %<-- Declare a tensor for size
T2 = symtensor(@ones, n,m); %<-- Declare a symtensor for size
rng('default'); %<- Setting random seed for reproducibility of this script

S2 = symktensor(r, T1) %<--Declare a random symktensor from tensor for size
S2 = symktensor(r, T2) %<--Declare a random symktensor from symtensor for size

S2 is a symktensor of order 2 and dimension 1
	S2.lambda = [ 1  1 ]
	S2.U = 
		    0.8147    0.9058
S2 is a symktensor of order 4 and dimension 3
	S2.lambda = [ 1  1 ]
	S2.U = 
		    0.1270    0.0975
		    0.9134    0.2785
		    0.6324    0.5469

This method of randomly generating a symktensor is useful when setting an initialization point in symmetric decomposition methods (i.e. cp_sym).

Lastly, a symktensor object can be declared from a vectorized version of the factor matrix and lambda vector, in which the lambda vector is stacked on top of a vectorized version of the factor matrix. The shape of the tensor must also be specified, by either passing a tensor/symtensor or listing the number of modes and the rank of the decomposition explicitly. Additionally, a 'nolambda' option can be added to any of these constructions, in which case the lambda vector should not be stacked onto the factor matrix.

V = [L; X(:)]; %<--Forming the vectorized version
S2 = symktensor(V, symtensor(@ones,m,n)) %<--size specified from symtensor

S2 = symktensor(X(:), symtensor(@ones,m,n), true) %<--'nolambda' option

S2 = symktensor(V, m, r) %<--size specified from modes and dimension

S2 = symktensor(X(:), m, r, true) %<--size from modes and dimension, 'nolambda' option

S2 is a symktensor of order 3 and dimension 4
	S2.lambda = [ 1 -1 ]
	S2.U = 
		     1     5
		     2     6
		     3     7
		     4     8
S2 is a symktensor of order 3 and dimension 4
	S2.lambda = [ 1  1 ]
	S2.U = 
		     1     5
		     2     6
		     3     7
		     4     8
S2 is a symktensor of order 3 and dimension 4
	S2.lambda = [ 1 -1 ]
	S2.U = 
		     1     5
		     2     6
		     3     7
		     4     8
S2 is a symktensor of order 3 and dimension 4
	S2.lambda = [ 1  1 ]
	S2.U = 
		     1     5
		     2     6
		     3     7
		     4     8

A symmetric Kruskal tensor can also be constructed directly from a generic Kruskal tensor in the ktensor format. If the Kruskal tensor is not symmetric, it is symmetrized by averaging the factor matrices and taking care to get the signs aligned.

K = ktensor(L, X-1, X+2, 2*X);
S2 = symktensor(K)

S2 is a symktensor of order 3 and dimension 4
	S2.lambda = [ 1  1 ]
	S2.U = 
		    1.2220   -6.5523
		    2.5685   -7.8311
		    3.9151   -9.1100
		    5.2616  -10.3889

This method of declaring a symktensor is useful in comparing decomposition methods: this constructor allows any decomposition method which generates a ktensor CP model to also generate a symktensor. In this way, decomposition methods which are non-symmetric in nature may easily be applied to symmetric problems.

Use ndims and size for the dimensions of a symktensor

For a given symktensor, ndims returns the number of dimensions (i.e. the number of modes) of the symmetric Kruskal tensor. size returns a size array of the symmetric Kruskal tensor.

%Declaring a symmetric Kruskal tensor
ndims(S)
size(S)

ans =

     3


ans =

     4     4     4

Use ncomponents for the rank of symktensor

The function ncomponents returns the number of components of a symktensor object. This is 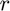$r$ in the symktensor's definition, the number of outer-product summands in the symmetric Kruskal tensor decomposition.

ncomponents(S)

ans =

     2

Use full to convert a symktensor to a tensor

The function full converts a symktensor to a tensor.

full(S)

ans is a symmetric tensor with 3 modes of dimension 4
	(1,1,1)  -124
	(1,1,2)  -148
	(1,1,3)  -172
	(1,1,4)  -196
	(1,2,2)  -176
	(1,2,3)  -204
	(1,2,4)  -232
	(1,3,3)  -236
	(1,3,4)  -268
	(1,4,4)  -304
	(2,2,2)  -208
	(2,2,3)  -240
	(2,2,4)  -272
	(2,3,3)  -276
	(2,3,4)  -312
	(2,4,4)  -352
	(3,3,3)  -316
	(3,3,4)  -356
	(3,4,4)  -400
	(4,4,4)  -448

Use double to convert a symktensor to a multi-dimensional array

The function double converts a symktensor to a multi-dimensional array.

double(S)

ans(:,:,1) =

  -124  -148  -172  -196
  -148  -176  -204  -232
  -172  -204  -236  -268
  -196  -232  -268  -304


ans(:,:,2) =

  -148  -176  -204  -232
  -176  -208  -240  -272
  -204  -240  -276  -312
  -232  -272  -312  -352


ans(:,:,3) =

  -172  -204  -236  -268
  -204  -240  -276  -312
  -236  -276  -316  -356
  -268  -312  -356  -400


ans(:,:,4) =

  -196  -232  -268  -304
  -232  -272  -312  -352
  -268  -312  -356  -400
  -304  -352  -400  -448

Basic operations with symktensors

Symktensors support multiplication by scalars. The result is the symktensor with the weight vector multiplied by the scalar.

4*S

ans is a symktensor of order 3 and dimension 4
	ans.lambda = [ 4 -4 ]
	ans.U = 
		     1     5
		     2     6
		     3     7
		     4     8

Use norm to compute the Frobenius norm of a symktensor

The function norm returns the Frobenius norm of a symktensor.

norm(S)

ans =

   2.1469e+03

Use normalize to normalize the components of a symktensor.

The function normalize divides each of the columns in a factor matrix by its vector 2-norm. The 2-norm weight is then absorbed into the weight vector of that column.

normalize(S)

ans is a symktensor of order 3 and dimension 4
	ans.lambda = [ 164.31677      2295.2176 ]
	ans.U = 
		    0.1826   -0.3790
		    0.3651   -0.4549
		    0.5477   -0.5307
		    0.7303   -0.6065

By passing an additional 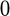$0$ argument to the normalize function, the weight vector is set to 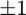$\pm 1$ and the weights are absorbed into the factor matrix.

normalize(S,0)

ans is a symktensor of order 3 and dimension 4
	ans.lambda = [ 1  1 ]
	ans.U = 
		    1.0000   -5.0000
		    2.0000   -6.0000
		    3.0000   -7.0000
		    4.0000   -8.0000

Use arrange to normalize and sort a symktensor

The function arrange normalizes the components of symktensor and sorts them according to the weight vector, in descending order.

arrange(S)
% Additionally, one can pass a permutation array of number of components of
% S. In this case the components are arranged according to the permutation.
arrange(S,[2 1])

ans is a symktensor of order 3 and dimension 4
	ans.lambda = [ 2295.2176      164.31677 ]
	ans.U = 
		   -0.3790    0.1826
		   -0.4549    0.3651
		   -0.5307    0.5477
		   -0.6065    0.7303
ans is a symktensor of order 3 and dimension 4
	ans.lambda = [ -1  1 ]
	ans.U = 
		     5     1
		     6     2
		     7     3
		     8     4

Computing the score of the match between two symktensors

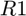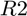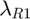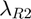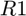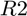The function score provides a measure of similarity between two symktensors. Given two symktensors $R1$ and $R2$, we denote by $\lambda_{R1}$ and $\lambda_{R2}$ their respective weight vectors and X and Y their respective factor matrices. The function score(R1,R2) first normalizes the symtensor. It then attempts to match the symktensor $R1$ to $R2$ and returns the following numeric quantification of their similarity.

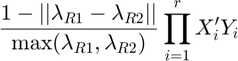
$$\frac{1 - ||\lambda_{R1}-\lambda_{R2}||}{\max(\lambda_{R1}, \lambda_{R2})} \prod_{i=1}^{r} X_{i}' Y_{i}$$

In the above formula, 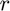$r$ is the number of components of 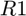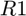$R1$. $R1$ must have at least as many components as 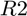$R2$. Any additional components are ignored in the score calculation. Since the formula for score depends on the arrangement of the components of 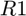$R1$, score rearranges 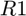$R1$ and tries a number of permuations. By default, 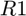$R1$ is rearranged by permuting indices greedily to increase the score. Calling score on two symktensors converts the symktensors to ktensors and calls the |score

R1 = symktensor([1; -1; 1], reshape(1:9, 3, 3), 3); %Declare some symtensors
R2 = symktensor([1; -1], reshape(1:6, 3,2), 3);

score(R1, R2) %The score is 1 (perfect match) because the 1st 2 components of R1 match those of R2

ans =

     1

Calling score on two symktensor converts the symktensors to ktensors and calls the score function for ktensor. See the ktensor/score documentation for more information.

Subscripted reference for symktensors

After defining a symktensor, one can reference its weight vector, factor matrix, or element using the following conventions. Note that elements are queried using multi-dimensional subscript notation, as opposed to linear.

S.lambda %<-- The weight vector
S.X %<-- The factor matrix

S(1,2,1) %<-- Generate the element of index (1,2,1) from the factorization

ans =

     1
    -1


ans =

     1     5
     2     6
     3     7
     4     8


ans =

  -148

Subscripted assignment for symktensors

Subscripted assignment can be used to change the order, weight vector, or factor matrix of a symktensor. First, we change the weight vector

S.lambda = [1;1]

S is a symktensor of order 3 and dimension 4
	S.lambda = [ 1  1 ]
	S.U = 
		     1     5
		     2     6
		     3     7
		     4     8

Next, we alter the factor matrix. U can be used instead of X in the notation that follows

S.X = [1 0; 0 1; 1 0; 0 1]

S is a symktensor of order 3 and dimension 4
	S.lambda = [ 1  1 ]
	S.U = 
		     1     0
		     0     1
		     1     0
		     0     1

Lastly, we alter the order. This changes 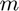$m$, in the 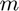$m$-way outer product expansion of a symmetric Kruskal tensor.

S.m = 4

S is a symktensor of order 4 and dimension 4
	S.lambda = [ 1  1 ]
	S.U = 
		     1     0
		     0     1
		     1     0
		     0     1

Tensor Toolbox for MATLAB: www.tensortoolbox.org.