All-at-once optimization for CP tensor decomposition
We explain how to use cp_opt function which implements the CP-OPT method that fits the CP model using direct or all-at-once optimization. This is in contrast to the cp_als function which implements the CP-ALS method that fits the CP model using alternating optimization. The CP-OPT method is described in the following reference:
- E. Acar, D. M. Dunlavy and T. G. Kolda, A Scalable Optimization Approach for Fitting Canonical Tensor Decompositions, J. Chemometrics, 25(2):67-86, 2011, http://doi.org/10.1002/cem.1335
This method works with any tensor that support the functions size, norm, and mttkrp. This includes not only tensor and sptensor, but also ktensor, ttensor, and sumtensor.
Contents
- Major overhaul in Tensor Toolbox Version 3.3, August 2022
- Optimization methods
- Optimization parameters
- Simple example problem #1
- Calling cp_opt method and evaluating its outputs
- Specifying different optimization method
- Calling cp_opt method with higher rank
- Simple example problem #2 (nonnegative)
- Call the cp_opt method with lower bound of zero
- Reproducibility
- Specifying different optimization method
Major overhaul in Tensor Toolbox Version 3.3, August 2022
The code was completely overhauled in the Version 3.3 release of the Tensor Toolbox. The old code is available in cp_opt_legacy and documented here. The major differences are as follows:
- The function being optimized is now
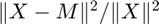 where X is the data tensor and M is the model. Previously, the function being optimized was
where X is the data tensor and M is the model. Previously, the function being optimized was 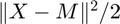 . The new formulation is only different by a constant factor, but its advantage is that the convergence tests (e.g., norm of gradient) are less sensitive to the scale of the X.
. The new formulation is only different by a constant factor, but its advantage is that the convergence tests (e.g., norm of gradient) are less sensitive to the scale of the X. - We now support the MATLAB Optimization Toolbox methods, fminunc and fmincon, the later of which has support for bound contraints.
- The input and output arguments are different. We've retained the legacy version for those that cannot easily change their workflow.
Optimization methods
The cp_opt methods uses optimization methods from other packages; see Optimization Methods for Tensor Toolbox. As of Version 3.3., we distribute the default method ('lbfgsb') along with Tensor Toolbox.
Options for 'method':
- 'lbfgsb' (default) - Uses L-BFGS-B by Stephen Becker, which implements the bound-constrained, limited-memory BFGS method. This code is distributed along with the Tensor Toolbox and will be activiated on first use. Supports bound contraints.
- 'lbfgs' - Uses POBLANO Version 1.2 by Evrim Acar, Daniel Dunlavy, and Tamara Kolda, which implemented the limited-memory BFGS method. Does not support bound constraints, but it is pure MATLAB and may work if 'lbfgsb' does not.
- 'compact' - Uses CR by Johannes Brust, which implements the limited-memory BFGS compact representation (CR) method. This code is distributed along with the Tensor Toolbox and will be activiated on first use. This is an alternative to Poblano.
- 'fminunc' or 'fmincon' - Routines provided by the MATLAB Optimization Toolbox. The latter supports bound constraints. (It also supports linear and nonlinear constraints, but we have not included an interface to those.)
Optimization parameters
The full list of optimization parameters for each method are provide in Optimization Methods for Tensor Toolbox. We list a few of the most relevant ones here.
- 'gtol' - The stopping condition for the norm of the gradient (or equivalent constrainted condition). Defaults to 1e-5.
- 'lower' - Lower bounds, which can be a scalar (e.g., 0) or a vector. Defaults to -Inf (no lower bound).
- 'printitn' - Frequency of printing. Normally, this specifies how often to print in terms of number of iteration. However, the MATLAB Optimization Toolbox method limit the options are 0 for none, 1 for every iteration, or > 1 for just a final summary. These methods do not allow any more granularity than that.
Simple example problem #1
Create an example 50 x 40 x 30 tensor with rank 5 and add 10% noise.
rng(1); % Reproducibility R1 = 5; problem1 = create_problem('Size', [50 40 30], 'Num_Factors', R, 'Noise', 0.10); X1 = problem1.Data; M1_true = problem1.Soln; % Create initial guess using 'nvecs' M1_init = create_guess('Data', X1, 'Num_Factors', R1, 'Factor_Generator', 'nvecs');
Calling cp_opt method and evaluating its outputs
Here is an example call to the cp_opt method. By default, each iteration prints the least squares fit function value (being minimized) and the norm of the gradient.
rng('default'); % Reproducibility [M1,~,info1] = cp_opt(X1, R1, 'init', M1_init, 'printitn', 25);
CP-OPT CP Direct Optimzation L-BFGS-B Optimization (https://github.com/stephenbeckr/L-BFGS-B-C) Size: 50 x 40 x 30, Rank: 5 Lower bound: -Inf, Upper bound: Inf Parameters: m=5, ftol=1e-10, gtol=1e-05, maxiters = 1000, subiters = 10 Begin Main Loop Iter 25, f(x) = 5.472721e-02, ||grad||_infty = 5.95e-04 Iter 49, f(x) = 9.809441e-03, ||grad||_infty = 5.72e-06 End Main Loop Final f: 9.8094e-03 Setup time: 0.00043 seconds Optimization time: 0.095 seconds Iterations: 49 Total iterations: 116 Exit condition: CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL.
It's important to check the output of the optimization method. In particular, it's worthwhile to check the exit message. The message CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH means that it has converged because the function value stopped improving. The message CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL means that the gradient is sufficiently small.
exitmsg = info1.optout.exit_condition; display(exitmsg);
exitmsg =
'CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL.'
The objective function here is different than for CP-ALS. That uses the fit, which is 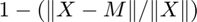 . In other words, it is the percentage of the data that is explained by the model. Because we have 10% noise, we do not expect the fit to be about 90%.
. In other words, it is the percentage of the data that is explained by the model. Because we have 10% noise, we do not expect the fit to be about 90%.
fit1 = 1 - sqrt(info1.f); display(fit1);
fit1 =
0.9010
We can "score" the similarity of the model computed by CP and compare that with the truth. The score function on ktensor's gives a score in [0,1] with 1 indicating a perfect match. Because we have noise, we do not expect the fit to be perfect. See doc score for more details.
scr1 = score(M1,M1_true); display(scr1);
scr1 =
0.9985
Specifying different optimization method
rng('default'); % Reproducibility [M1b,~,info1b] = cp_opt(X1, R1, 'init', M1_init, 'printitn', 25, 'method', 'compact');
CP-OPT CP Direct Optimzation
CR solver (limited-memory) (https://github.com/johannesbrust/CR)
Size: 50 x 40 x 30, Rank: 5
Parameters: m=5, gtol=1e-05, maxiters = 1000 subiters = 500
Begin Main Loop
Compact Representation (ALG0)
Line-search: wolfeG
V-strategy: s
n= 600
--------------------------------
k nf fk ||gk|| step iexit
0 1 9.87861e-01 2.00132e-02 1.000e+00 0
25 34 5.52331e-02 1.71379e-03 1.000e+00 1
50 67 9.81030e-03 1.64187e-04 1.000e+00 1
End Main Loop
Final f: 9.8094e-03
Setup time: 0.00029 seconds
Optimization time: 0.066 seconds
Iterations: 58
Total iterations: 76
Exit condition: Convergence: Norm tolerance
Check exit condition
exitmsg = info1b.optout.exit_condition; display(exitmsg); % Fit fit1b = 1 - sqrt(info1b.f); display(fit1b); % Score scr1b = score(M1b,M1_true); display(scr1b);
exitmsg =
'Convergence: Norm tolerance'
fit1b =
0.9010
scr1b =
0.9986
Calling cp_opt method with higher rank
Re-using the same example as before, consider the case where we don't know R in advance. We might guess too high. Here we show a case where we guess R+1 factors rather than R.
% Generate initial guess of the correct size rng(2); M1_plus_init = create_guess('Data', X1, 'Num_Factors', R1+1, ... 'Factor_Generator', 'nvecs');
% Run the algorithm rng('default'); % Reproducibility [M1c,~,output1c] = cp_opt(X1, R1+1, 'init', M1_plus_init,'printitn',25);
CP-OPT CP Direct Optimzation L-BFGS-B Optimization (https://github.com/stephenbeckr/L-BFGS-B-C) Size: 50 x 40 x 30, Rank: 6 Lower bound: -Inf, Upper bound: Inf Parameters: m=5, ftol=1e-10, gtol=1e-05, maxiters = 1000, subiters = 10 Begin Main Loop Iter 25, f(x) = 5.462523e-02, ||grad||_infty = 6.90e-04 Iter 50, f(x) = 9.788408e-03, ||grad||_infty = 1.11e-05 Iter 65, f(x) = 9.775966e-03, ||grad||_infty = 7.19e-06 End Main Loop Final f: 9.7760e-03 Setup time: 0.00021 seconds Optimization time: 0.057 seconds Iterations: 65 Total iterations: 146 Exit condition: CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL.
% Check exit condition exitmsg1c = output1c.optout.exit_condition; display(exitmsg1c); % Fit fit1c = 1 - sqrt(output1c.f); display(fit1c); % Check the answer (1 is perfect) scr1c = score(M1c, M1_true); display(scr1c);
exitmsg1c =
'CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL.'
fit1c =
0.9011
scr1c =
0.9985
Simple example problem #2 (nonnegative)
We can employ lower bounds to get a nonnegative factorization. First, we create an example 50 x 40 x 30 tensor with rank 5 and add 10% noise. We select nonnegative factor matrices and lambdas. The create_problem doesn't really know how to add noise without going negative, so we hack it to make the observed tensor be nonzero.
R2 = 5; rng(3); problem2 = create_problem('Size', [50 40 30], 'Num_Factors', R2, 'Noise', 0.10,... 'Factor_Generator', 'rand', 'Lambda_Generator', 'rand'); X2 = problem2.Data .* (problem2.Data > 0); % Force it to be nonnegative M2_true = problem2.Soln;
Call the cp_opt method with lower bound of zero
Here we specify a lower bound of zero with the last two arguments.
rng('default'); % Reproducibility [M2,M20,info2] = cp_opt(X2, R2, 'init', 'rand','lower',0,'printitn',25); % Check the output exitmsg2 = info2.optout.exit_condition; display(exitmsg2); % Check the fit fit2 = 1 - sqrt(info2.f); display(fit2); % Evaluate the output scr2 = score(M2,M2_true); display(scr2);
CP-OPT CP Direct Optimzation
L-BFGS-B Optimization (https://github.com/stephenbeckr/L-BFGS-B-C)
Size: 50 x 40 x 30, Rank: 5
Lower bound: 0, Upper bound: Inf
Parameters: m=5, ftol=1e-10, gtol=1e-05, maxiters = 1000, subiters = 10
Begin Main Loop
Iter 25, f(x) = 1.607417e-02, ||grad||_infty = 1.85e-03
Iter 50, f(x) = 1.023857e-02, ||grad||_infty = 5.09e-04
Iter 75, f(x) = 9.791157e-03, ||grad||_infty = 1.44e-04
Iter 100, f(x) = 9.775862e-03, ||grad||_infty = 1.04e-04
Iter 108, f(x) = 9.775178e-03, ||grad||_infty = 1.10e-04
End Main Loop
Final f: 9.7752e-03
Setup time: 0.00038 seconds
Optimization time: 0.078 seconds
Iterations: 108
Total iterations: 225
Exit condition: CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL.
exitmsg2 =
'CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL.'
fit2 =
0.9011
scr2 =
0.9929
Reproducibility
The parameters of a run are saved, so that a run can be reproduced exactly as follows.
rng(6); % Different random state
cp_opt(X2,R2,info2.params);
CP-OPT CP Direct Optimzation L-BFGS-B Optimization (https://github.com/stephenbeckr/L-BFGS-B-C) Size: 50 x 40 x 30, Rank: 5 Lower bound: 0, Upper bound: Inf Parameters: m=5, ftol=1e-10, gtol=1e-05, maxiters = 1000, subiters = 10 Begin Main Loop Iter 25, f(x) = 1.607417e-02, ||grad||_infty = 1.85e-03 Iter 50, f(x) = 1.023857e-02, ||grad||_infty = 5.09e-04 Iter 75, f(x) = 9.791157e-03, ||grad||_infty = 1.44e-04 Iter 100, f(x) = 9.775862e-03, ||grad||_infty = 1.04e-04 Iter 108, f(x) = 9.775178e-03, ||grad||_infty = 1.10e-04 End Main Loop Final f: 9.7752e-03 Setup time: 0.00035 seconds Optimization time: 0.1 seconds Iterations: 108 Total iterations: 225 Exit condition: CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL.
Specifying different optimization method
rng('default'); % Reproducibility [M2b,~,info2b] = cp_opt(X2, R2, 'init', M20, 'printitn', 25, ... 'method', 'compact', 'lower', 0);
CP-OPT CP Direct Optimzation
CR solver (limited-memory) (https://github.com/johannesbrust/CR)
Size: 50 x 40 x 30, Rank: 5
Parameters: m=5, gtol=1e-05, maxiters = 1000 subiters = 500
Begin Main Loop
Compact Representation (ALG0)
Line-search: wolfeG
V-strategy: s
n= 600
--------------------------------
k nf fk ||gk|| step iexit
0 1 3.86664e+00 2.40555e+00 1.000e+00 0
25 29 1.57093e-02 7.62420e-03 1.000e+00 1
50 54 1.03890e-02 2.97993e-03 1.000e+00 1
75 81 9.81333e-03 7.01183e-04 1.000e+00 1
100 109 9.77713e-03 2.66092e-04 1.000e+00 1
125 136 9.77473e-03 2.67276e-05 1.000e+00 1
End Main Loop
Final f: 9.7747e-03
Setup time: 0.00016 seconds
Optimization time: 0.16 seconds
Iterations: 137
Total iterations: 149
Exit condition: Convergence: Norm tolerance
% Check exit condition exitmsg2b = info2b.optout.exit_condition; display(exitmsg2b); % Fit fit2b = 1 - sqrt(info2b.f); display(fit2b); % Score scr2b = score(M2b,M2_true); display(scr2b);
exitmsg2b =
'Convergence: Norm tolerance'
fit2b =
0.9011
scr2b =
0.9935
